SOLUCIÓN AL PROBLEMA 4.3

1.- La constante de equilibrio K_P viene determinada por la expresión:

DGº = - R*T*lnK_P

Por otra parte, la variación de energía libre de Gibbs en condiciones estándar (DGº) de la reacción viene dada por la relación:

DGº = DHº - T*DSº

De los datos termodinámicos que aporta el problema, se calcula:

DHº = 112 kJ/mol

DSº = 132 J/(mol*K)

Así, se tienen:

DGº (298K) = 72,66 kJ/mol. Por tanto, K_P (298K) = 1,8*10^-13

DGº (773K) = 9,96 kJ/mol. Por tanto, K_P (773K) = 0,21

De la relación :

K_P = K_C * (RT)^Dn, donde en este caso la variación de moles en fase gas de la reacción es +1, se llega a:

K_C (298K) = 7,4*10^-15

K_C (773K) = 3,3*10^-3

2.-

	COCl2 (g)	<--->	Cl2 (g)	+	CO (g)
concentraciones en equilibrio:	C0 (1-a )		C0*a		C0*a

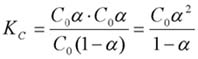
La aproximación K_C » C₀*a ² no es adecuada en ninguno de los dos casos que plantea el problema. Resolviendo las correspondientes ecuaciones cuadráticas, se obtiene:

2.1.- Si C₀ = 1,0 M entonces, a = 0,056 , se descompone el 5,6%.

2.2.- Si C₀ = 1,0*10^-4 M entonces, a = 0,97 , se descompone el 97%.

3.1.- Si aumenta la temperatura, el equilibrio se desplaza hacia la derecha, porque la reacción es endotérmica (DHº> 0). Se comprueba por ejemplo por el aumento de la constante de equilibrio calculado en el apartado 1, al pasar de 25ºC a 500ºC.

3.2.- Si aumenta la presión, el equilibrio se desplaza hacia la izquierda, porque así disminuye el número de moles en fase gas.