SOLUCIÓN AL PROBLEMA 2.1

Para realizar los cálculos, es necesario conocer el volumen de la bombilla, que se considera una esfera. Se obtiene así V= 0,113 L, para aplicar en p*V = n*R*T.

Para conocer el número de átomos en fase gas a cada temperatura, se aplicará la ecuación de Clausius Clapeyron que relaciona las presiones de vapor de un sólido a dos temperaturas:

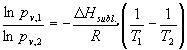
Con los dos datos de presiones de vapor que aporta el problema, se obtienen DH_subl.=186 kcal/mol, y con este valor, se pueden obtener ya los resultados:

A 25ºC (298K) ---> p_v = e^-297 atm ---> n= 0 moles ---> 0 átomos W en fase gas

A 3000ºC (3273K) ---> p_v = 1,2*10^-6 atm ---> n= 5,0*10^-10 moles ---> 3,0*10¹⁴ átomos W en fase gas

Comentario: en ambos casos el número de átomos en fase gas es muy pequeño (aunque 3,0*10¹⁴ puedan parecer muchos átomos, representan sólo 9*10^-8 g de W), dado que es un sólido muy poco volátil. Es especialmente llamativo que haya 0 átomos en fase gas a 25ºC, pero se debe tener en cuenta:

1.- La presión de vapor (equilibrio W(sólido) « W (vapor) es muy pequeña (e^-297 atm).

2.- Se ha utilizado un valor de variación de entalpía de sublimación, calculado entre 3000 y 3500 K, para obtener la presión de vapor a 298 K, con lo que se supone constante esa variación de entalpía en un intervalo muy amplio de temperaturas.